Industrial noise
Industrial noise is usually considered mainly from the point of view of environmental health and safety, rather than nuisance, as sustained exposure can cause permanent hearing damage. Traditionally, occupational noise has been a hazard linked to heavy industries such as ship-building and associated only with noise induced hearing loss (NIHL). Modern thinking in occupational safety and health identifies noise as hazardous to worker safety and health in many places of employment and by a variety of means.
Noise can not only cause hearing impairment (at long-term exposures of over 85 decibels (dB), known as an exposure action value), but it also acts as a causal factor for stress and raises systolic blood pressure.
Additionally, it can be a causal factor in work accidents, both by masking hazards and warning signals, and by impeding concentration.
Noise also acts synergistically with other hazards to increase the risk of harm to workers. In particular, noise and dangerous substances (e.g. some solvents) that have some tendencies towards ototoxicity may give rise to rapid ear damage.
A-weighted measurements are commonly used to determine noise levels that can cause harm to the human ear, and special exposure meters are available that integrate noise over a period of time to give an Leq value (equivalent sound pressure level), defined by standards.
Industrial noise reduction
Acoustic quieting is the process of making machinery quieter by damping vibrations to prevent them from reaching the observer.
When two identical industrial noise sources are side by side producing a recorded noise at 100 dB(A) the reduction in noise from shutting off one of the noise sources is about 3 dB resulting in 97 dB(A).
When one doubles the distance from a noise source the recorded noise level is reduced by 6 dB. This is also called the Rule of 6. This is based on the fact that the equation to calculate noise attenuation at a distance 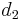 , knowing the SPL at distance
, knowing the SPL at distance 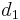 is given by
is given by ![10log_{10}\left[\left(\frac{d_2}{d_1}\right)^2\right] = 20log_{10}\left[\frac{d_2}{d_1}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/da02ed114897d92d7d27b08a9adee0b6.png) , where d is the distance. If the distance is doubled, the equation simplifies to
, where d is the distance. If the distance is doubled, the equation simplifies to 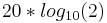 which equals 6.02 (or approx. 6)
which equals 6.02 (or approx. 6)
See also
- Earplug
- Earmuffs
- Noise health effects
- Noise control
- Noise mitigation
- Noise pollution
- Noise regulation
- Protective clothing
- A-weighting
- ITU-R 468 noise weighting
- Weighting filter
- Equal-loudness contour
- Safe-In-Sound Award Excellence in Hearing Loss Prevention